Table of Contents

Testing of various catch standard deviations --- q, s, M locked

For the model with latent variables for the catch data, we conduct the following experiments, all of which are done with this data set. First, the model without latent variables is run. The values for the catchability, standard deviation of the survey indices and the mortality are used as constants in the model with latent variables, which is run for various levels on the standard deviation of the catch data. Since most of the variable values are locked, the confidence intervals produced by the model are very small.

We test the following standard deviations on the catch: 0.05, 0.1, 0.15, 0.2 and 0.25.

For each run we report the misfit, which we define to be

misfit = sum_{All observations} 0.5 * ( log(I) - log(qN) )2

In other words, the smaller this number is, the better the survey indices match the estimated stock size. As one can see, this number decreases when the standard deviation of the catch increases, with sc = 0.05 as the only exception.

:!: The estimates of the cohort sizes are more or less the same for all choices of sc.

:!: As sc increases, the absolute value of the likelihood function value decreases.

Exact catch

  Non-RE misfit:      1.820

The estimates and trajectories are:

Num. cohorts Trajectories Estimates
4 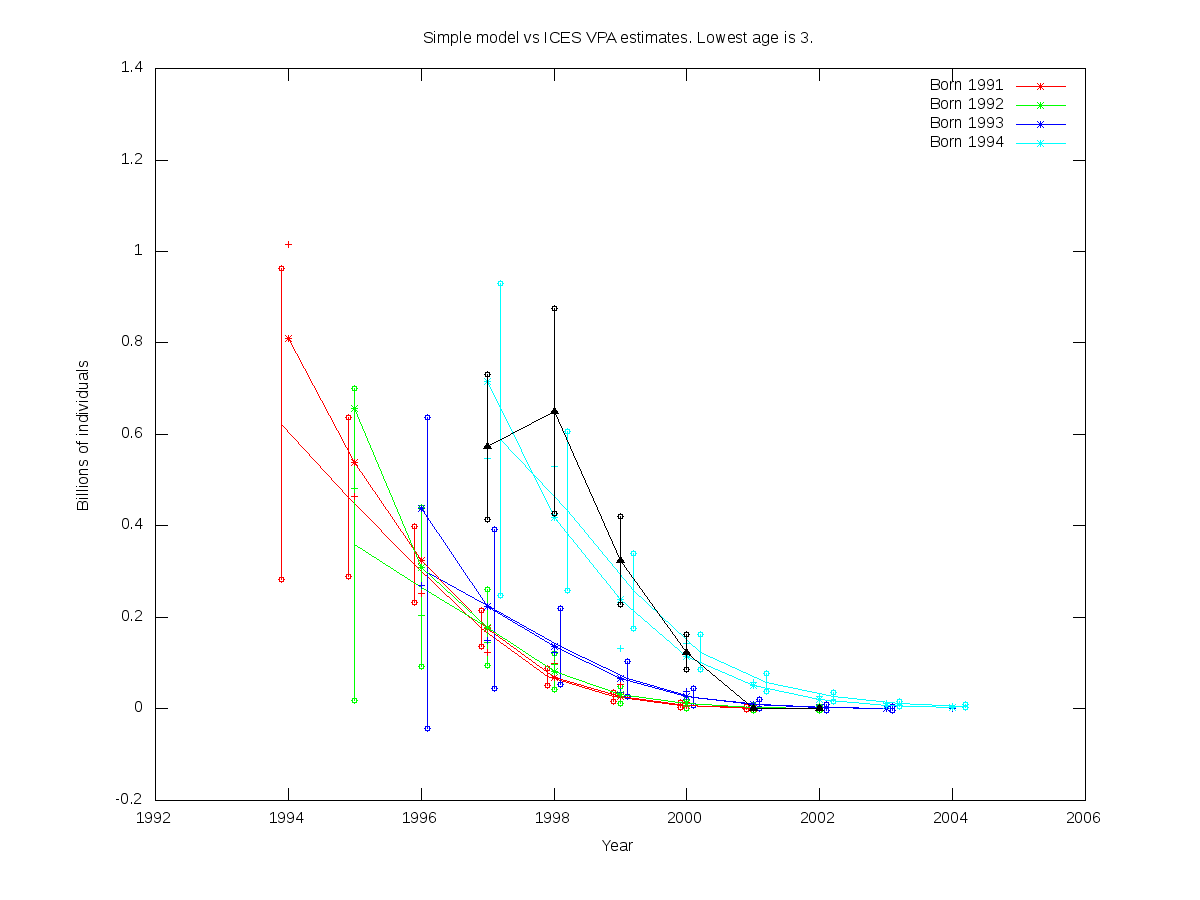Non-RE parfile:
cod.par
../simple_model_sdreport/cod.par is the user-defined function defined from: ../simple_model_sdreport/cod.par
 
# Number of parameters = 7  Objective function value = -18.7801  Maximum gradient component = 0.000328611
# N0:
 0.622791 0.359443 0.298084 0.589102
# q:
 0.344332
# logs:
-1.08687795940
# M:
0.286208904677

sc = 0.05

  RE misfit:      1.882
Num. cohorts Trajectories Estimates
4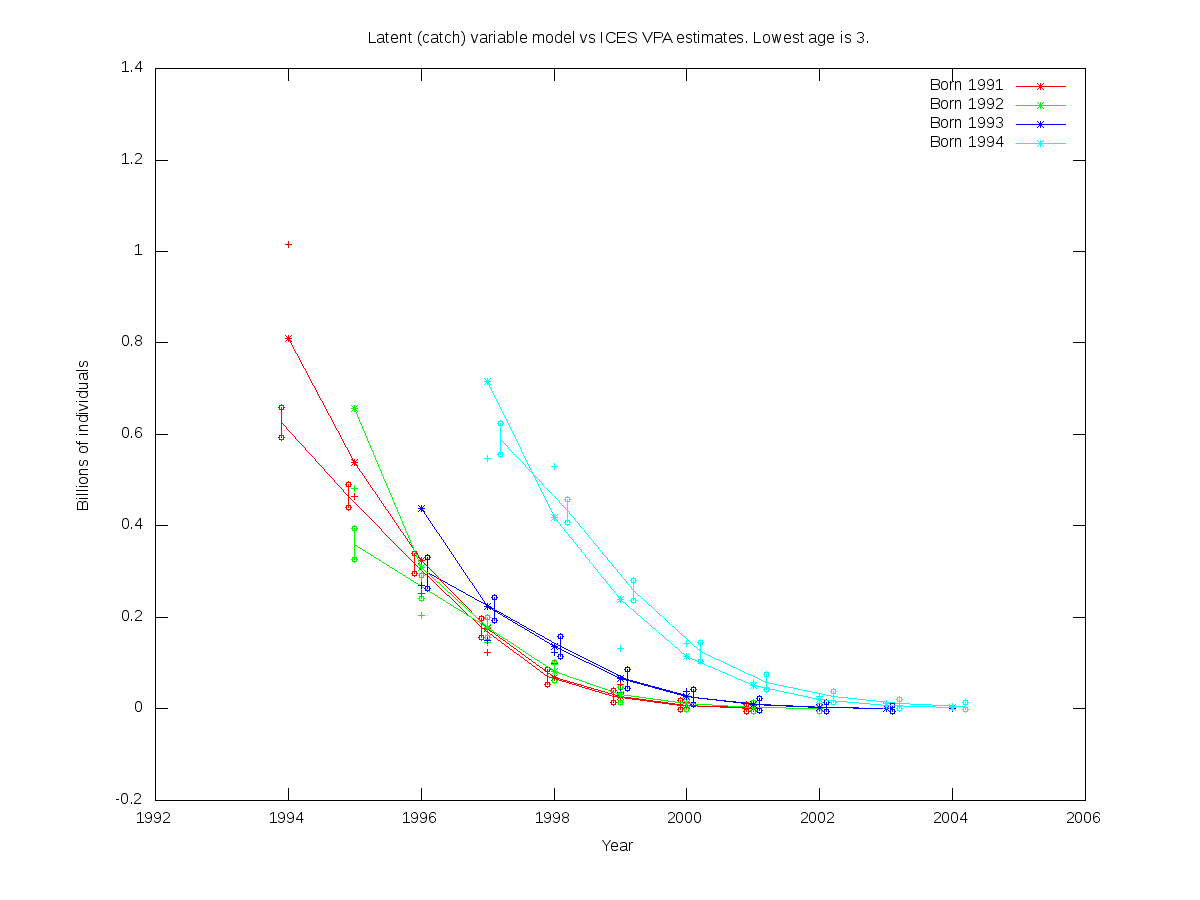
cod.par
# Number of parameters = 4  Objective function value = -41.3135  Maximum gradient component = 3.18128e-05
# N0:
 0.625798 0.360217 0.297445 0.589751
# q:
 0.344330
# logs:
-1.08690000000
# M:
0.286210000000
# logscc:
-2.99570000000
# ce:
 0.00607677727972 0.0527881327035 0.108236829066 0.0716351134276 0.111304699438 0.248520863778 0.250954553656 0.00507665924228 0.0273474982545 0.0514526137138 0.0791632153292 0.0512822216301 0.172997445434 -0.0326570725038 0.00642843203800 0.0134611094072 0.00822862264096 -0.120526715382 0.0129580571379 -0.0757812682532 -0.0395552748756 0.00444283876465 0.0593327324051 -0.0238705619626 0.00677922350320 0.00217447025335 0.00811096130120 -0.000525125519077

sc = 0.1

  RE misfit:      1.765
Num. cohorts Trajectories Estimates
4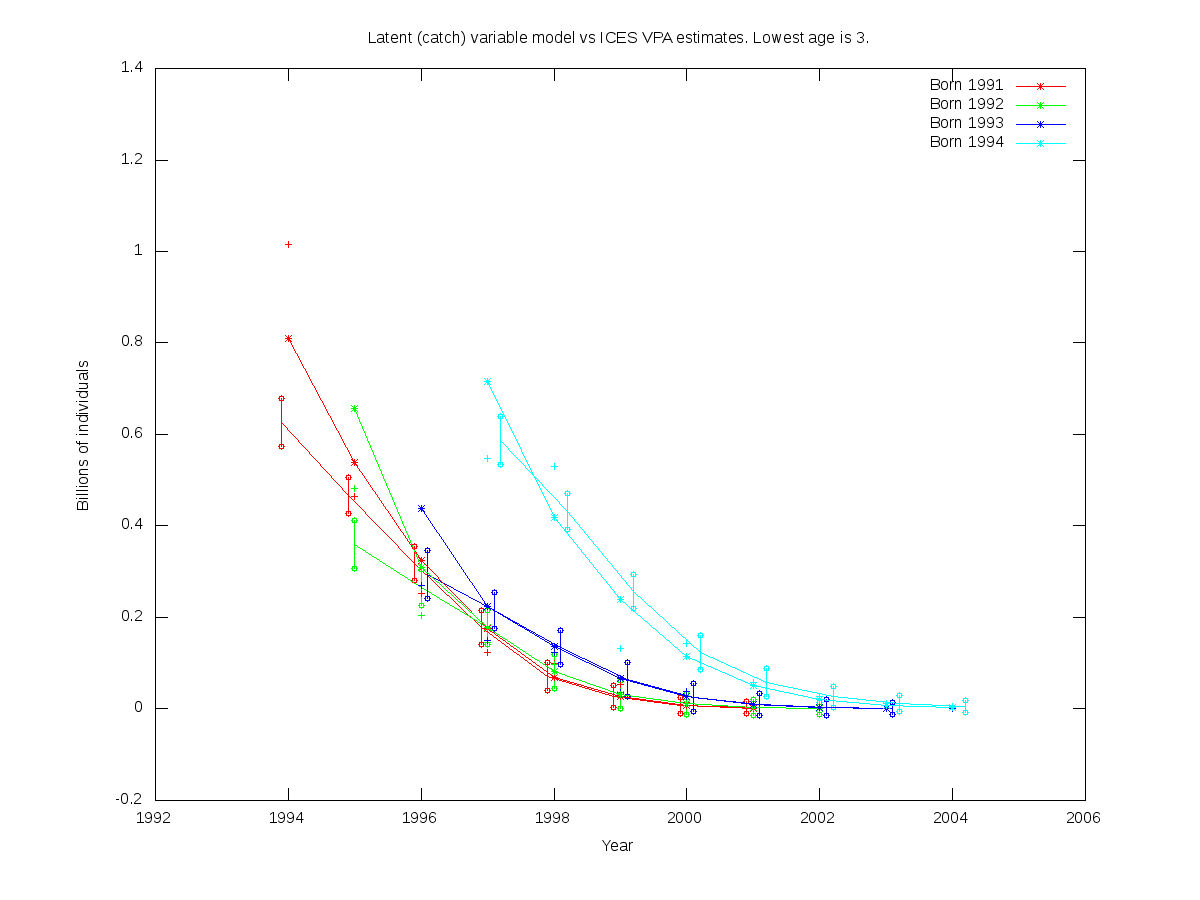
cod.par
# Number of parameters = 4  Objective function value = -39.1030  Maximum gradient component = 6.59749e-07
# N0:
 0.626847 0.359398 0.293274 0.586739
# q:
 0.344330
# logs:
-1.08690000000
# M:
0.286210000000
# logscc:
-2.30260000000
# ce:
 0.00717371386508 0.0623024987881 0.106838500149 -0.00727841853676 0.133422491700 0.438642102107 0.487122821330 0.00557205734436 0.0189230169446 -0.0115898109589 0.0687880035532 0.0546275293727 0.318954924968 -0.0737794027901 0.00392062069876 -0.0281553619299 -0.0767931533848 -0.308320458142 -0.0103735113069 -0.165205557798 -0.0825936963613 0.00558668464994 0.0896514206481 -0.0864720201540 -0.0114903454906 -0.0101960849496 0.00806135028380 -0.00265801930885

sc = 0.15

  RE misfit:      1.661
Num. cohorts Trajectories Estimates
4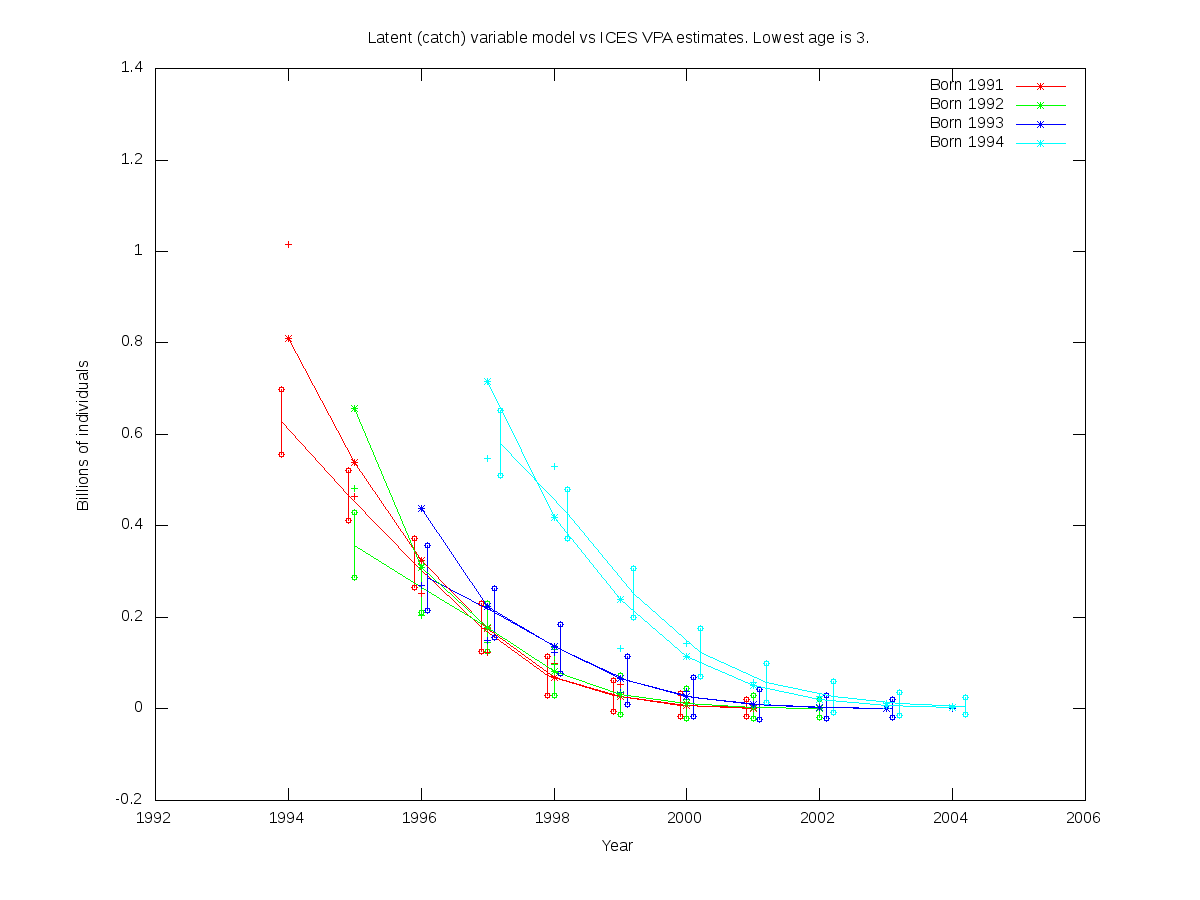
cod.par
# Number of parameters = 4  Objective function value = -37.8395  Maximum gradient component = 8.42471e-05
# N0:
 0.627756 0.358000 0.287267 0.580884
# q:
 0.344330
# logs:
-1.08690000000
# M:
0.286210000000
# logscc:
-1.89710000000
# ce:
 0.00874495514757 0.0760265461654 0.115882157306 -0.0707826286747 0.151430209660 0.611123044389 0.717677634190 0.00681978747091 0.0169088880577 -0.0517818229251 0.0740424294426 0.0625218779776 0.463932951854 -0.114733356896 0.00297546617756 -0.0567185172784 -0.129556977585 -0.449898032102 -0.00965238424925 -0.231960325692 -0.114328666724 0.00485844416478 0.105422304293 -0.163748016705 -0.0380416440742 -0.0255873228041 0.00740885850240 -0.00459962718646

sc = 0.20

  RE misfit:      1.543
Num. cohorts Trajectories Estimates
4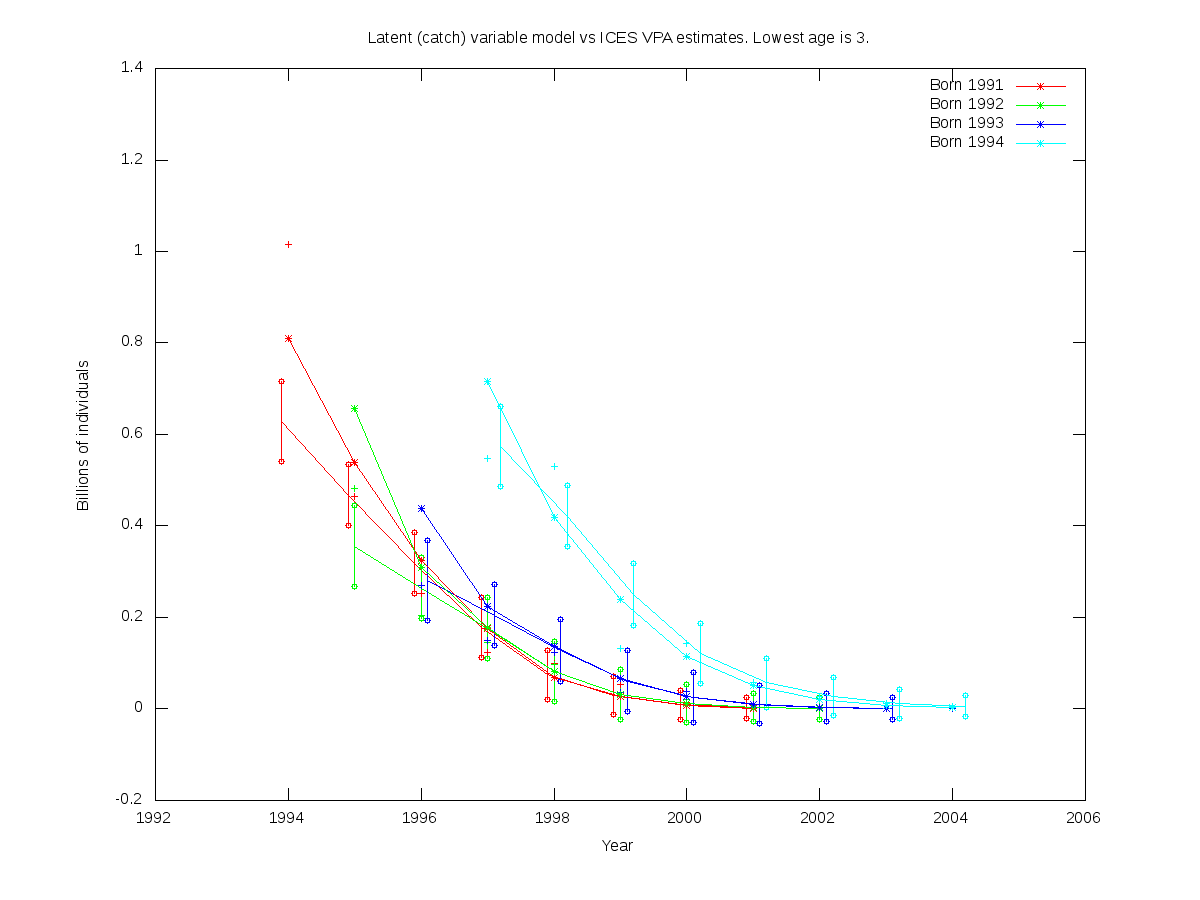
cod.par
# Number of parameters = 4  Objective function value = -37.0410  Maximum gradient component = 7.82529e-08
# N0:
 0.628473 0.356175 0.280516 0.573662
# q:
 0.344330
# logs:
-1.08690000000
# M:
0.286210000000
# logscc:
-1.60940000000
# ce:
 0.0105945326672 0.0924150565958 0.131672733003 -0.122988529089 0.160092228320 0.754206722089 0.932703965414 0.00833505245764 0.0176928559663 -0.0801478682914 0.0857703374823 0.0690610265861 0.601980358685 -0.156020358537 0.00299342620150 -0.0754628415649 -0.155311268816 -0.548969360875 0.0133179595988 -0.276253970069 -0.134205773273 0.00439542206215 0.127236667450 -0.225951783363 -0.0529266402812 -0.0313054265443 0.0140114328999 -0.00454072712752

sc = 0.25

  RE misfit:      1.420
Num. cohorts Trajectories Estimates
4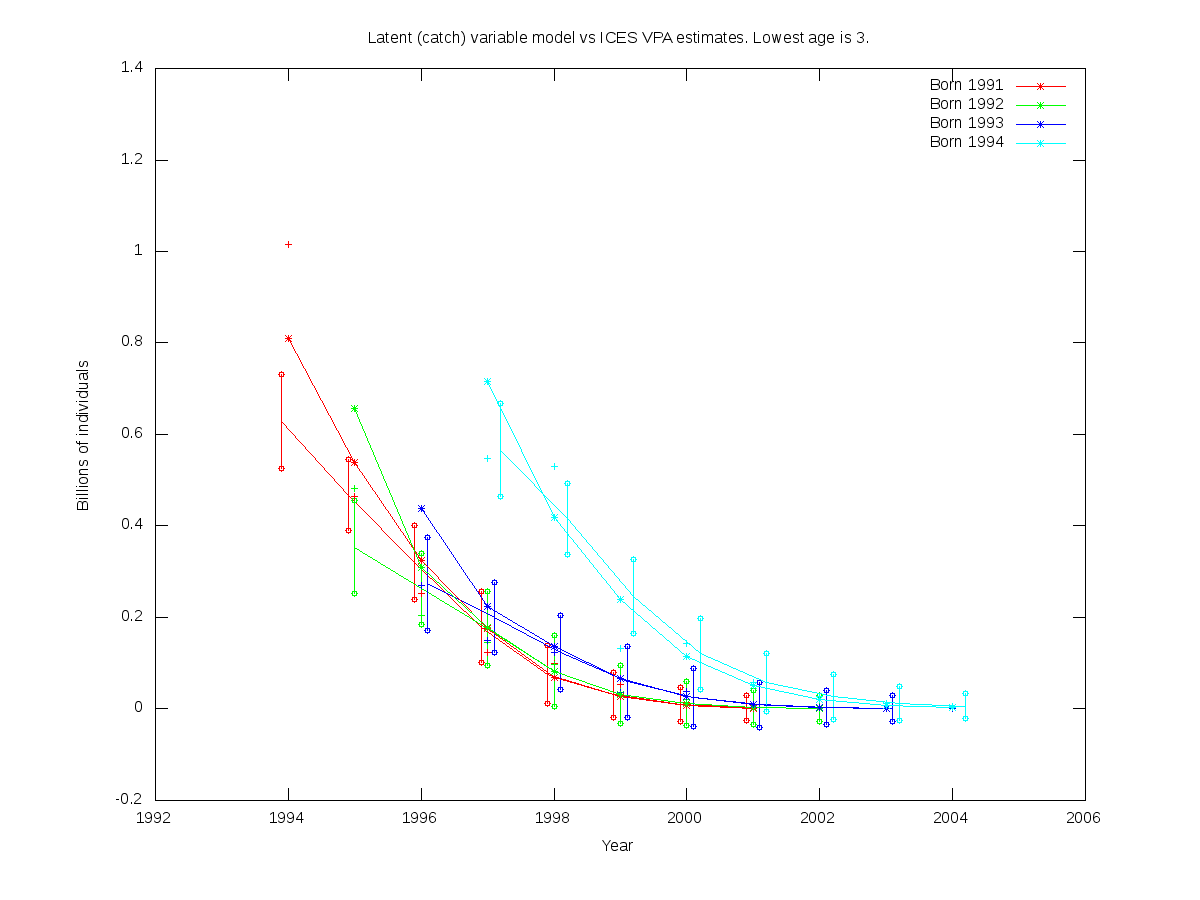
cod.par
# Number of parameters = 4  Objective function value = -36.4879  Maximum gradient component = 0.000174743
# N0:
 0.628747 0.354038 0.273783 0.565967
# q:
 0.344330
# logs:
-1.08690000000
# M:
0.286210000000
# logscc:
-1.38630000000
# ce:
 0.0125564588907 0.110250222202 0.151499565938 -0.166635957021 0.158328129982 0.861012158619 1.11894581604 0.00996117587657 0.0201967149377 -0.0998994921814 0.101236517714 0.0722938204005 0.728453096543 -0.196792494711 0.00360153715761 -0.0867820061536 -0.159657096149 -0.613204271138 0.0543741927850 -0.301492912920 -0.143405877135 0.00427958102293 0.156243372877 -0.271969861788 -0.0555966832440 -0.0271598469491 0.0279294136297 -0.00242007305686